Jabłoń

Limit czasu: 1s | Limit pamięci: 128MB

Jaś ma jabłoń, która jest ukorzenionym w wierzchołku $1$ drzewem. W niektórych wierzchołkach tego drzewa rosną jabłka. Jaś będzie trząsł jabłonią, dopóki wszystkie jabłka nie znajdą się w liściach. Za każdym razem, kiedy Jaś trzęsie jabłonią dla każdego jabłka:

• jeżeli dane jabłko jest w liściu nic się z nim nie dzieje.
• jeżeli dane jabłko nie jest w liściu spada do jednego z synów wierzchołka, w którym się znajduje.

Na ile różnych sposobów jabłka mogą ustawić się w liściach? (jabłka są rozróżniane)

Wejście

Pierwszy wiersz zawiera jedną liczbę przypadków testowych $t$. W następnych wierszach opisane są kolejno przypadki testowe w formacie:

• Pierwszy wiersz zawiera dwie liczby naturalne $n$ i $k$ oznaczające odpowiednio liczbę wirzchołków jabłoni i liczbę jabłek.
• Kolejne $n-1$ wierszy zawira opis jabłonki. W każdym z tych wierszy znajdują się dwie liczby $u_i$ i $v_i$ oznaczające, że istnieje krawędź między wierzchołkami $u_i$ i $v_i$.
• Ostatni wiersz zawiera $k$ liczb całkowitych $a_i$ odzielonych pojedynczymi odstępami. Są to numery wierzchołków, w których znajdują się jabłka.

Wyjście

Na wyjściu powinno znaleźć się $t$ wierszy, zawierających po jednej liczbie całkowitej – odpowiedzi na kolejne przypadki testowe modulo $10^9+7$ w kolejności podawania na wejściu.

Ograniczenia

• Wszystkie liczby na wejściu są całkowite i dodatnie.
• Suma $n$ we wszystkich przypadkach testowych nie przekroczy $10^6$.
• Suma $k$ we wszystkich przypadkach testowych nie przekroczy $10^6$.
• $1 \le u_i, v_i, a_i \le n$

Przykłady

Wejście 1

1
5 3
1 2
2 3
3 4
3 5
1 3 5

Wyjście 1

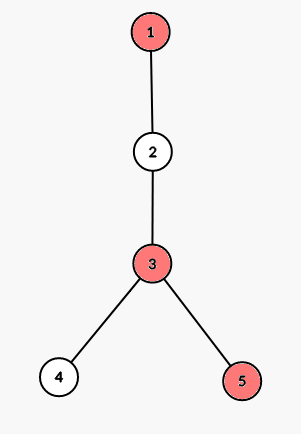
4

Wyjaśnienie 1

Drzewo z testu przykładowego pokazane jest na rysunku (czerowne wierzchołki oznaczają jabłka):