Triangulacja

Limit czasu: 0.5s | Limit pamięci: 64MB

Dany jest wielokąt prosty. Znajdź jedną z jego poprawnych triangulacji.

Triangulacją nazwiemy pewien podział wielokąta na niezdegenerowane trójkąty, który spełnia poniższe warunki (wszystkie jednocześnie):

• każdy wierzchołek każdego trójkąta jest wierzchołkiem wielokąta,
• każdy bok wielokąta musi być bokiem dokładnie jednego trójkąta,
• pole części wspólnej każdych dwóch trójkątów wynosi zero,
• suma pól wszystkich trójkątów jest równa polu wielokąta,
• każdy trójkąt musi całkowicie zawierać się w wielokącie,
• każdy bok każdego trójkąta musi zawierać dokładnie dwa wierzchołki wielokąta.

Wejście

Pierwszy wiersz wejścia zawiera jedną liczbę całkowitą $n$, oznaczającą liczbę wierzchołków wielokąta.

Następne $n$ wierszy zawiera po dwie liczby całkowite $x_i, y_i$, oznaczające odciętą oraz rzędną $i$-tego wierzchołka wielokąta. Wierzchołki $i$ oraz $i+1$ sąsiadują ze sobą dla $i = 1, 2, ..., n-1$. Wierzchołki $n$ oraz $1$ także są ze sobą sąsiadują. Zagwarantowane jest, że podany wielokąt jest prosty.

Wyjście

Pierwszy wiersz wyjścia powinien zawierać jedną liczbę całkowitą $m$, oznaczającą liczbę wybranych przekątnych.

Następne $m$ wierszy powinno zawierać po dwie liczby całkowite $a_i$ oraz $b_i$, oznaczające że $i$-ta wybrana przekątna zaczyna się w $(x[a_i], y[a_i])$, a kończy w $(x[b_i], y[b_i])$ (w tym miejscu indeksujemy od zera).

Poza tym, że podany zbiór przekątnych powinien dzielić wielokąt zgodnie z opisem triangulacji w treści, powinny być także sepłnione dodatkowe warunki:

• $1 \le m \le 5\,000$,
• $0 \le a_i, b_i < n$,
• $a_i \neq b_i$,
• podana przekątna nie może być bokiem wielokąta,
• podane przekątne powinny być parami różne.

Ograniczenia

• $4 \le n \le 1\,000$
• $-10^9 \le x_i, y_i \le 10^9$

Przykłady

Wejście 1

4
0 0
5 0
5 5
0 5

Przykładowe wyjście 1

1
0 2

Wejście 2

18
0 0
10 7
12 3
20 8
13 17
10 12
12 14
14 9
8 10
6 14
10 15
7 18
0 16
1 13
3 15
5 8
-2 9
5 5

Przykładowe wyjście 2

15
1 3
1 15
1 17
3 7
3 15
4 6
4 7
7 15
8 15
9 11
9 14
9 15
11 14
12 14
15 17

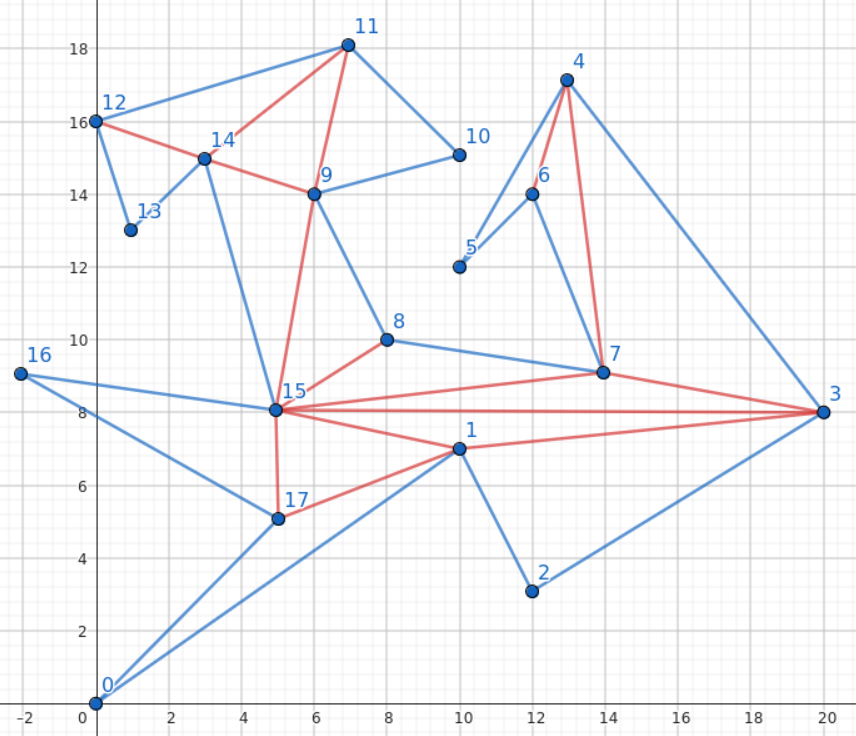
Wyjaśnienie 2: Sytuację przedstawia rysunek: